- A Thesis Proposal Presented to The Academic Faculty by Wei (Tina) Zhuo
- In Partial Fulfillment of PHD Degree in Computer Science in the School of Interactive Computing
- Oct 2013
Bending with Local Volume Preservation
Date
(TBD) Link to Doodle: http://doodle.com/bz2gi7sqibzk6zvz
Committee
Professor Stefanie Hahmann, Applied Mathematics, Grenoble Institute of Technology
Professor Karen Liu, Interactive Computing, Georgia Institute of Technology
Professor Jarek Rossignac (Advisor), Interactive Computing, Georgia Institute of Technology
Professor Greg Turk, Interactive Computing, Georgia Institute of Technology
Abstract
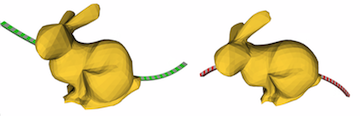
A bending is the effect of applying a continuous, spatially-varying transformation to a solid. It is controlled by a low dimensional proxy, which can be a spine curve or surface. In this thesis, we address a suite of problems in bending with local volume preservation, meaning that the transformation preserves the volume of any subset of the solid. Our bending framework adopts the following assumptions in mechanics:
- Planes normal to the spine curve remain normal to the spine curve after bending.
- Lines normal to the spine surface remain normal to the spine surface after bending.
With these assumptions, we derive a family of closed-form solutions for bending with local volume preservation. The derivation exploits the constraint of unit Jacobian determinant. The solutions can be computed in real-time using analytic geometry. We discuss anticipated applications in shape manipulation, animation, and geometric modeling of machining process.
Proposal Material
pdf, ppt, video
last updated: Oct 3, 2013
Related Publication
Wei Zhuo and Jarek Rossignac, "Fleshing: Spine-driven Bending with Local Volume Preservation", Computer Graphics Forum (CGF), VOL. 32, NO. 2, 2013 (Presented at EG 2013)
Wei Zhuo and Jarek Rossignac, "Curvature-based Offset Distance: Implementation and Applications", Computer & Graphics (C&G), VOL. 36, NO. 5: 445–454, 2012 (Presented at SMI 2012)